How to Convert Decimal to Binary?

In computers, all data is ultimately represented using binary numbers. We need convert Decimal to Binary.

1. Conversion steps:

1. Divide the number by 2.
2. Get the integer quotient for the next iteration.
3. Get the remainder for the binary digit.
4. Repeat the steps until the quotient is equal to 0.

We can now explain how decimal numbers are converted to binary by giving an example.

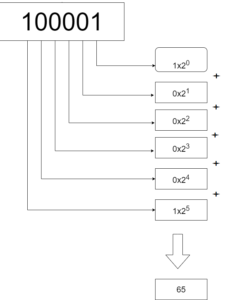
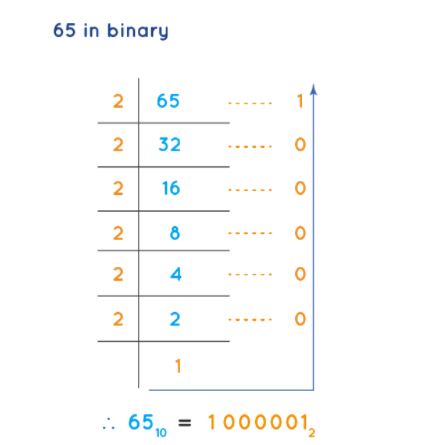
In binary, 65 is represented as 1000001. Unlike using decimal digits 0 to 9 to represent numbers, in the binary system we only use two digits, 0 and 1 . We use 7 bits to represent 65 in binary.

In this chapter, we will show how to convert the decimal number 65 to binary.

• 65 in Binary:65_₁₀ = 1000001_₂
• 65 in Octal:65_₁₀ = 101_₈
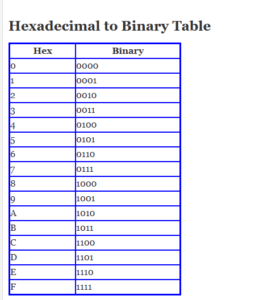
• 65 in Hexadecimal:>65_₁₀ = 41_₁₆
• 1000001_₂  in Decimal:6_₁₀

Here are the steps to convert the decimal number 65 to binary:

1. Divide 65 by 2, the quotient is 32 and the remainder is 1.
2. Divide 32 by 2, the quotient is 16 and the remainder is 0.
3. Divide 16 by 2, the quotient is 8 and the remainder is 0.
4. Divide 8 by 2, the quotient is 4 and the remainder is 0.
5. Divide 4 by 2, the quotient is 2 and the remainder is 0.
6. Divide 2 by 2, the quotient is 1 and the remainder is 0.
7. Divide 1 by 2, the quotient is 0 and the remainder is 1.

Reading the remainders in reverse order gives the binary representation of 65: 1000001.

Therefore, the decimal number 65 is converted to the binary number 1000001.

 

2. Decimal to Binary Conversion Table

Decimal Number	Binary Number	Hex Number
0	0	0
1	1	1
2	10	2
3	11	3
4	100	4
5	101	5
6	110	6
7	111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F
16	10000	10
17	10001	11
18	10010	12
19	10011	13
20	10100	14
21	10101	15
22	10110	16
23	10111	17
24	11000	18
25	11001	19
26	11010	1A
27	11011	1B
28	11100	1C
29	11101	1D
30	11110	1E
31	11111	1F
32	100000	20
64	1000000	40
128	10000000	80
256	100000000	100